We can debate the pros and cons of one development process over another until we're blue in the face, but the simple fact is that we will never declare a true winner. There simply is no silver bullet development process that will help every development team deliver every product on time and on budget. This article provides a brief overview of three development processes and when they are most appropriate.
Trendy development processes come and go, but the debate over which software development process is “best” never seems to end. At almost any industry conference today, you’re sure to hear someone condemning the waterfall process, proclaiming that design is dead, or wondering if process is even relevant considering today’s compressed project timelines. In my opinion, you can gain a lot more from retiring the “Which development process (if any) is best?” question forever, and replacing it with a slightly different one: “Which development process is best for my project?”
We can debate the pros and cons of one development process over another until we’re blue in the face, but the simple fact is that we will never declare a true winner. Why? Because different processes have different strengths and weaknesses. There is no silver bullet development process that will help every development team deliver every product on time and on budget. Likewise, there is no “good for nothing” development process. Each development process is viable and useful, but each one works better in some situations than it does in others.
Moreover, most companies (in my estimate, about eighty percent of them) do not really have any development process in place—even if they think they do. A development process that’s on paper is not sufficient. For a development process to be useful, it must be implemented and followed on a daily basis. But before you start worrying about which development process is best, you should implement some kind of defined, repeatable process in your organization. One thing is for certain: any development process is better than no development process.
What Process Works Where?
If you’re working on a somewhat traditional project (for instance, an accounting system) where the features are defined a priori and it’s possible to freeze the specification, the waterfall process is your best bet. The waterfall development process starts with one long design phase that defines the entire project and all of the product’s features; this phase typically includes requirements analysis. Once the design is set in stone, the implementation phase begins. After all features described in the design phase are implemented, they are integrated into a working product. Finally, the product is tested, and then it is shipped to customers. The flow of these phases is represented in Figure 1.
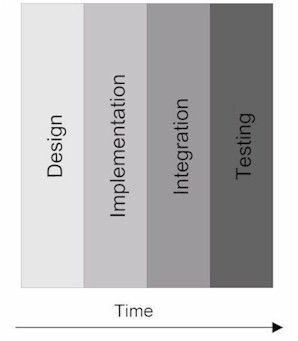
Figure 1: The waterfall process moves through each phase of development until final releaseWhen you adopt the waterfall process, you define the project's scope up front and try not to change it. As a result, you have the information required to set a realistic schedule and budget, and you're typically free from the surprises that often throw projects off track. That's why the waterfall process is typically the most efficient and economic choice if you are building a well-defined system. However, it's not feasible in all situations. Often, it's impossible to define a project's scope up front—especially if you're working on a truly ground-breaking project. Many of the teams working on ground-breaking projects start off with no concrete idea of what the final product will look like, or change directions midstream. If these teams refrained from revising their projects' scope because they believed revisions were not allowed in their development process, they would most likely end up with less impressive products…or none at all. In this case, the waterfall model that typically works so well for more stable products would end up being an obstacle to the project's success.
The Spiral and Incremental Processes
If you're working on a project whose nature and scope are vague or unpredictable (for example, a project where you cannot determine your next steps until you have reached a certain plateau), consider either a spiral or incremental process. These two processes are very similar in that both involve a series of many frequent iterations of the design-implementation-integration-test cycle seen in the waterfall process; the general flow of these frequent iterations is shown in Figure 2. In the spiral process, you have many short iterations of this cycle, many of which refine the same features over and over again. In the incremental process, you also have many short iterations of this cycle, but here each cycle implements different features that the customer requests or you deem appropriate.
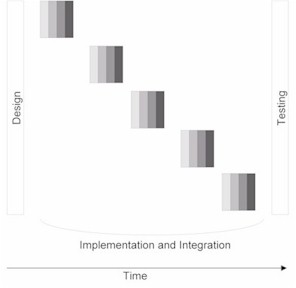
Figure 2: The spiral and iterative processes both contain many frequent design/implementation/integration/testing cycles
The spiral process works best if you have a ground-breaking project of undefined scope and plan on continually redefining and perfecting particular features throughout the course of the project. The incremental process is better suited for situations where you have some general project direction, but you plan on continually redefining the product by adding different features to it. Both processes are well suited to innovative projects because their short iterations allow the team to quickly show the customer the results of the latest request. This allows for rapid feedback on the success of the most recent iteration and the direction of the next one. Such frequent and rapid feedback is not necessary for traditional projects, but is the lifeblood of innovative ones.Using Processes as Tools
Once you've decided which general paradigm suits your current project—or even all of the projects in your foreseeable future—you're not free to ignore all the others. Different aspects of other development processes can be used as tools to help you achieve certain goals. Just as (I hope!) you would consider using different development tools to solve different issues you face during development, you should consider borrowing different aspects of "other" development processes where appropriate. For example, if you're working on an innovative project and decide to include a well-defined feature, use a waterfall model for that aspect of the project. Or, if you're working on a well-defined waterfall project and find that the code's quality is somewhat lacking, why not try to improve the quality of the code you are producing by adopting the pair programming and unit testing techniques integral to Extreme Programming, one popular spin on the incremental process?
In projects that span years, different processes might be used as tools at different phases of the product's lifecycle. In such lengthy projects, the "best" process often depends upon the product's maturity. For example, at my company, development teams usually work with the spiral, incremental, and waterfall development paradigms throughout the evolution of a project.
We realize that we cannot predict exactly what users and the market will demand of a new product from day one, so we don't start with the waterfall model. Rather, we start with shorter, more frequent iterations in an effort to elicit a lot of feedback in the earliest stages. This way, we can learn what the users need and react accordingly. Typically, when we start developing something fresh out of research and development, we need the ability to quickly prototype the most critical features and determine whether the product will work. Our highest priority is implementing the most complicated and uncertain technologies in an attempt to flush the unknowns critical to the technology that will drive the product. In these situations, the spiral process suits us well: we implement a feature, see how it works, reimplement it, and keep repeating this cycle until we have implemented the most complicated part of the technology, and the product has sufficient features to make this technology attractive to the user. At this point, iterations are a matter of days.
After we release a 1.0 version of a product, our users often offer many useful ideas about product features and functionality. Generally, our technologies are right on target, but our presentation of the technologies could be enhanced to better meet user needs. Because of the sheer amount of feedback we receive at this point, we cannot implement all the good ideas in a single short cycle. Instead, we respond to this feedback over a period of time. We collect this information, turn it into feature requests, and then enter these requests into our bug-tracking system. Next, we prioritize the features and decide which ones will be implemented in which subsequent releases. These features are then implemented incrementally throughout the next series of releases. Here, we are using an incremental model because although we know which features we need to implement, we are not certain how they should be implemented.
Once we have completed a number of releases, we gain a deep understanding of the market and the users' needs. We understand the technology, have flushed the previously unknown aspects of the technology, and do not need to perform the extensive amounts of research that we did in the earlier stages of the project. After we achieve this understanding, we shift to a waterfall process, where the cycle for each release typically spans about six to eight months. At this point, the waterfall process works well because we can define the work that needs to be done up front, we really understand the code structure and layout, and we can foresee how new features need to be built.In the ideal world, all developers would master all development processes so that they could easily determine when another practice would help them, then execute the appropriate practice flawlessly. In reality, it's actually not that difficult to master a variety of different development processes. After all, you've probably noticed that the three major development processes share the same four fundamental phases: design, implementation, integration, and testing. The main differences between these three processes are the length of the phases and the features implemented in each phase.
If you get a good grasp on each of these four common phases and what practices can be applied to improve and expedite each one, you will have the skills required to execute these phases independently of length. In any process, you need to integrate practices into these four phases that will prevent errors from destroying your process and the software it produces. Once you're able to do this, you should be able to work effectively within any of the main development paradigms.

